【数学】静岡市葵区の中学３年生へ！相似な図形の応用問題の解き方！～比合わせの利用～

静岡市葵区・駿河区で塾をお探しの皆さん。こんにちは！

思考力学習・ミス防止を徹底指導。集団指導の学習塾WINGSです。

葵小・横内小・竜南小・城北小・伝馬町小・安東小・静大附属小・服織小・森下小

城内中・東中・安東中・大成中

静岡東高校・駿河総合高校の方々にお世話になっております。

内申点に関わる事実上最後の定期テストを控えている静岡市葵区の中学３年生へ！

相似な図形の応用問題を解く上で必須なテクニック、比合わせを伝授します！

本当に高得点を目指したい中学３年生は、是非最後までご覧ください。

４つの点が並んだ時は比合わせの利用！

過去、東中のテストで役に立った比合わせですが、

使いどころは点が４つ並んだ時の比を求めたい時です！

(１)の比は砂時計型１つで１：４とすぐに求まります。

問題は(２)で、中途半端な位置にあるＰＱ：ＱＣの比の求め方です！

全長ＡＣに注目すると、点がＡ、Ｐ、Ｑ、Ｃと４つ並んでいることが分かりますよね？

この条件の時に限って、今回ご紹介する比合わせが有効になります！

以下、どのようにＰＱ：ＱＣの比を求めていくのか、詳しく解説いたします。

1. 砂時計型を１つ見つける

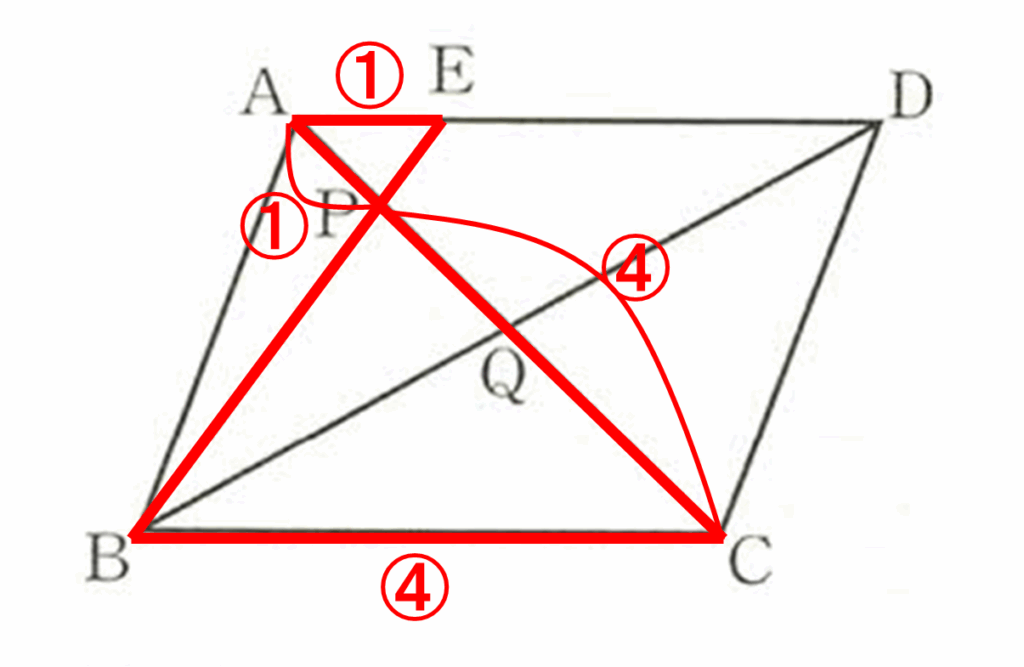
※本当は○と□などで分けないといけませんが、記号が少ないのでご容赦ください

(１)を求めるために使用した砂時計型から、ＡＰ：ＰＣ＝１：４が分かります。

ＰＱ：ＱＣは求まりませんが、近しい比はこれで分かりましたね！

2. ２つ目の砂時計型を見つける

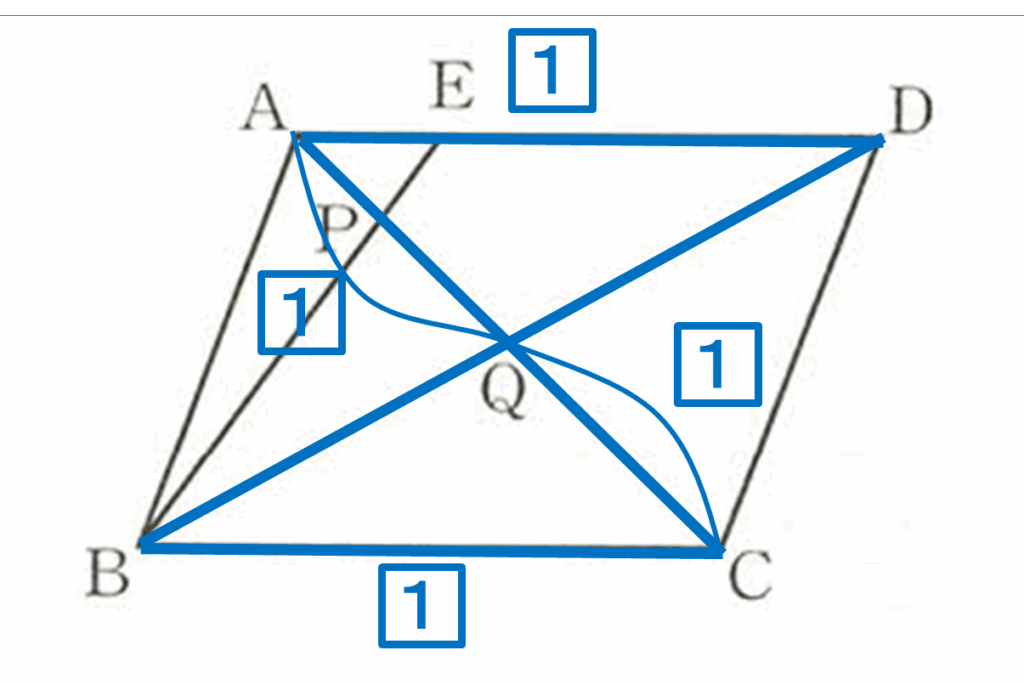
図形をよく見てください！砂時計型は１つではありません！

求めたい線分を含んだピラミッド型or砂時計型を２つ見つけてください！

ＡＱ：ＱＣ＝１：１と、まだ答えは出ませんが、またまた近しい比が分かりましたね。

3. ２つの比を１つの比に合わせる

最後に、この○と□の２種類の比を１つに揃えます！

これが比合わせというテクニックです！

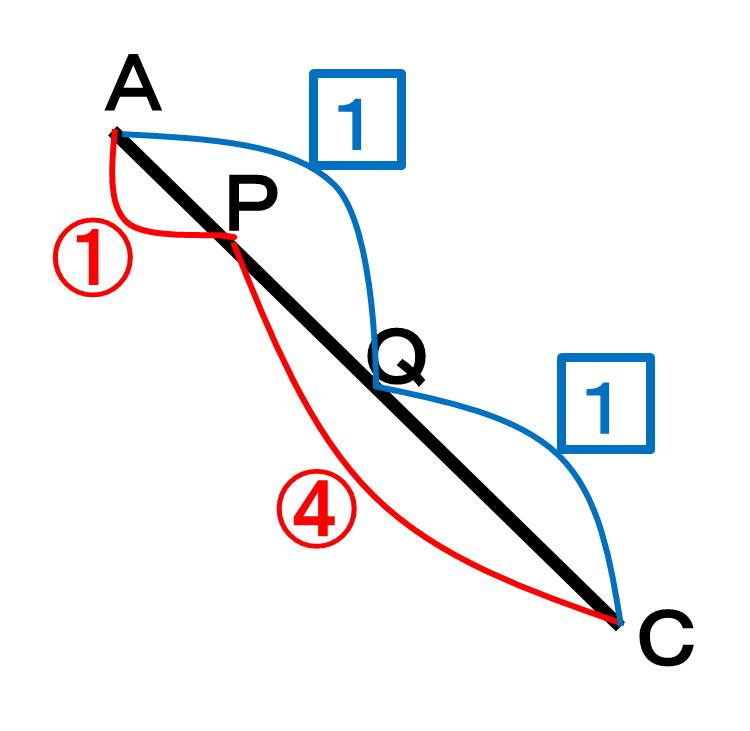
現状、２つの砂時計型から上記のような比が求まっています。

○と□で分け方は異なりますが、全長はＡＣと共通しています！

このようにすることで、○の比と□の比を、共通の◇の比に揃えることができます！

○は１：４を保ちながら２倍、□は１：１を保ちながら５倍します。

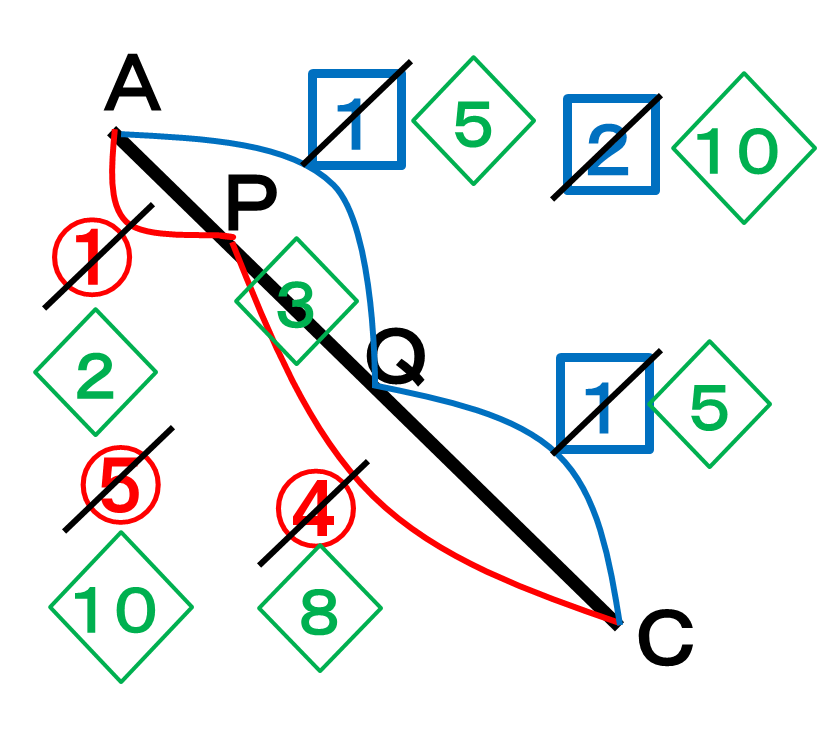
ＰＱはＡＱ－ＡＰ(もしくはＰＣ－ＱＣ)で比を求め、ＰＱ：ＱＣ＝３：５が正解になります！

最後に

これが過去、東中の後期中間テストで役に立った比合わせというテクニックです。

理解すれば少し練習するだけで使いこなせるようになりますよ！

同様の問題を張っておくので、是非高得点を目指している中学３年生は練習してみてください！

答えは、２番が３：４、３番(１)１０：３、(２)６：７、４番が５：９です。

次回も相似な図形の応用問題が解けるようになるブログを更新します。

今回のブログで少しでもご興味をお持ちいただけた方、是非WINGSの授業を体験してみてください！

学習相談・無料体験から受け付けておりますので、まずは気軽にホームページから資料請求をしてください。

お問い合わせはホームページの問い合わせフォーム、または054-330-9913までお願いします。

ブログを見ました・友達から聞きました・看板を見ました・チラシを見ました。とお伝えください。

【↓新年特別キャンペーン実施中↓】