【数学】静岡市葵区の中学３年生へ！相似な図形の応用！～補助線の引き方のポイント～

静岡市葵区・駿河区で塾をお探しの皆さん。こんにちは！

思考力学習・ミス防止を徹底指導。集団指導の学習塾WINGSです。

葵小・横内小・竜南小・城北小・伝馬町小・安東小・静大附属小・服織小・森下小

城内中・東中・安東中・大成中

静岡東高校・駿河総合高校の方々にお世話になっております。

前回に引き続き数学の相似な図形の応用について解説します。

今回は過去作をいじった『補助線の引き方』についてポイントを伝授します！

前回⇒【数学】静岡市葵区の中学３年生へ！相似な図形の応用問題の解き方！～比合わせの利用～

補助線の引き方の３つのポイント

では早速問題です。

求めたい比が一直線上に並んでいることが分かります。

この問題設定がすでに答えへの解き方を指示しています！

一直線上の比は『ピラミッド型』か『砂時計型』から求めるしかありません！

しかし困ったことに、ＡＤを含んだピラミッドも砂時計も見つかりません...

ここで補助線の出番です！補助線の引き方のポイントですが、

①求めたい線分をいじらない

②ピラミッド型・砂時計型をつくる

③図形の外部へ突き抜ける

上記３つを意識してどんな補助線が有効かを考えていきましょう！

1. 求めたい線分をいじらない

補助線の引き方のポイントではなく、まずは引いてはいけない補助線の解説です。

そもそも補助線は、問われている線分の比を求めるために必要です。

その求めたい線分を切ったり伸ばしたりしてしまうような補助線は不適切です！

これでは仮にＢＧ：ＡＥの比が分かっても、ＡＦ：ＦＤは求まりませんよね...

線分ＡＤはそのまま残すような補助線を考えてみましょう！

2. ピラミッド型・砂時計型をつくる

大事なことなので繰り返しますが、補助線は『ピラミッド型』か『砂時計型』を作るように引きます。

そしてこれらの形をつくるためには、平行線を意識することがポイントになります！

一つ補助線を引いて、ピラミッド型を作ってみましょう！

惜しいですね～...ＡＤが底辺以外ならいけたかもしれません。

※ＢＣに平行な線をＦを通るように引くのは線分ＡＤをいじるのでＮＧです

図形の内部に補助線を引いてもうまく答えが出ない...そんな時は？

3. 図形の外部を突き抜ける

相似な図形の応用問題では、図形の外部に突き抜けるような補助線が有効になってきます。

次は外部へ突き抜け、砂時計型を作ってみます。

これで直接ＡＦ：ＦＤを求めるのではなく、ＡＧ：ＤＢを求め答えを代用することができます！

次の問題は、飛び出したＡＧのＢＤに対する比です。注目する図形を変えましょう。

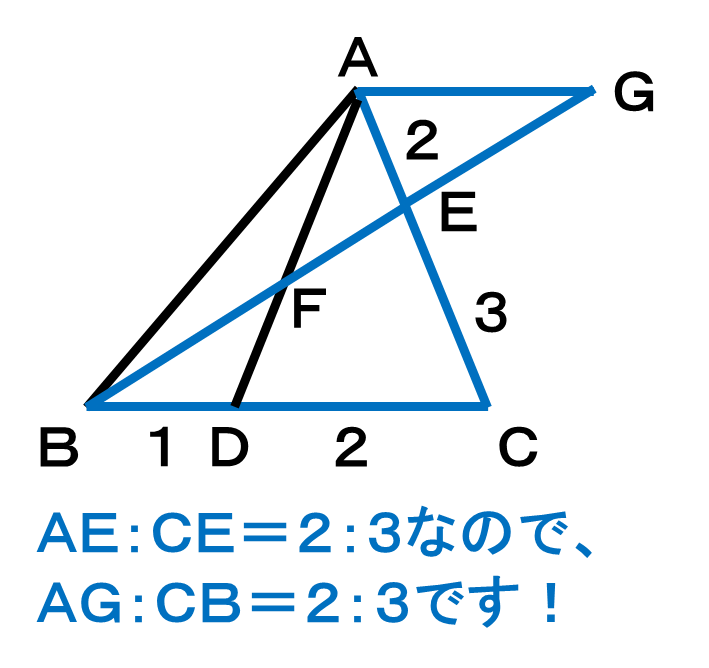
ちょうどＣＢがあわせて３なので、ＡＧの比はそのまま２で良いですね！

※仮にＣＢの比が４ならば、比を調整する必要があります

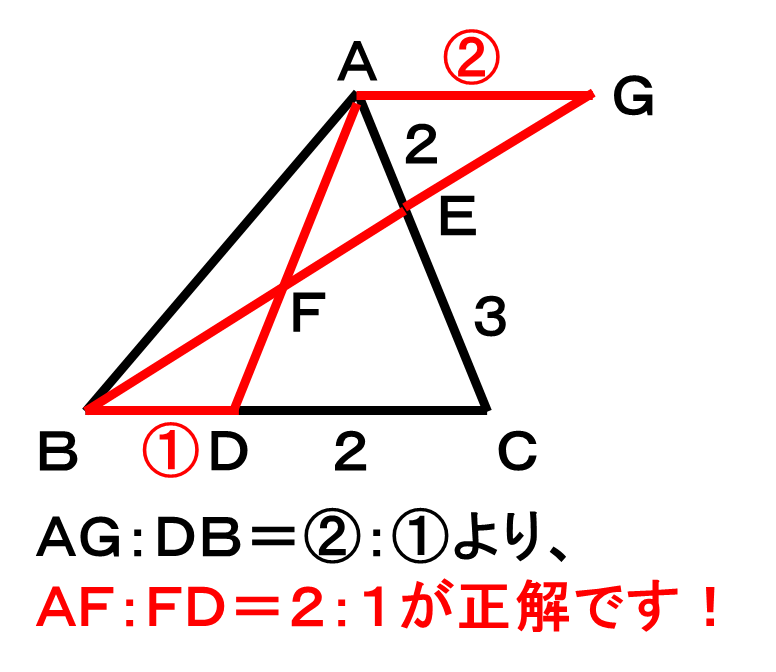
まとめ

以上が補助線の引き方の３つのポイントでした。

①求めたい線分をいじらない

②ピラミッド型・砂時計型をつくる

③図形の外部へ突き抜ける

入試問題はその先で比合わせが必要になったりもします。

図形問題はいろいろな考え方を駆使しながら解けるので練習のやり甲斐がありますね！

知識・考え方を理解したらいろいろな問題を解いて応用してみましょう！

今回のブログで少しでもご興味をお持ちいただけた方、是非WINGSの授業を体験してみてください！

学習相談・無料体験から受け付けておりますので、まずは気軽にホームページから資料請求をしてください。

お問い合わせはホームページの問い合わせフォーム、または054-330-9913までお願いします。

ブログを見ました・友達から聞きました・看板を見ました・チラシを見ました。とお伝えください。

【↓新年特別キャンペーン実施中↓】