【数学】一次関数と二次関数の融合問題!~一次関数の直線の式を一瞬で求める裏技~
静岡市葵区・駿河区で塾をお探しの皆さん。こんにちは!
思考力学習・ミス防止を徹底指導。集団指導の学習塾WINGSです。
葵小・横内小・竜南小・城北小・伝馬町小・安東小・静大附属小・服織小・森下小
城内中・東中・安東中・大成中
静岡東高校・駿河総合高校の方々にお世話になっております。
前回、二次関数の基本を完全攻略できるブログをアップしました。
【数学】これ一本で静岡県の基本問題は大丈夫!~二次関数の変域と変化の割合の求め方~
今回はもう少し突っ込んだ、一次関数の直線の式を一瞬で求める裏技を伝授します!
一次関数の直線の式を一瞬で求める裏技
まずは問題設定から確認しましょう。
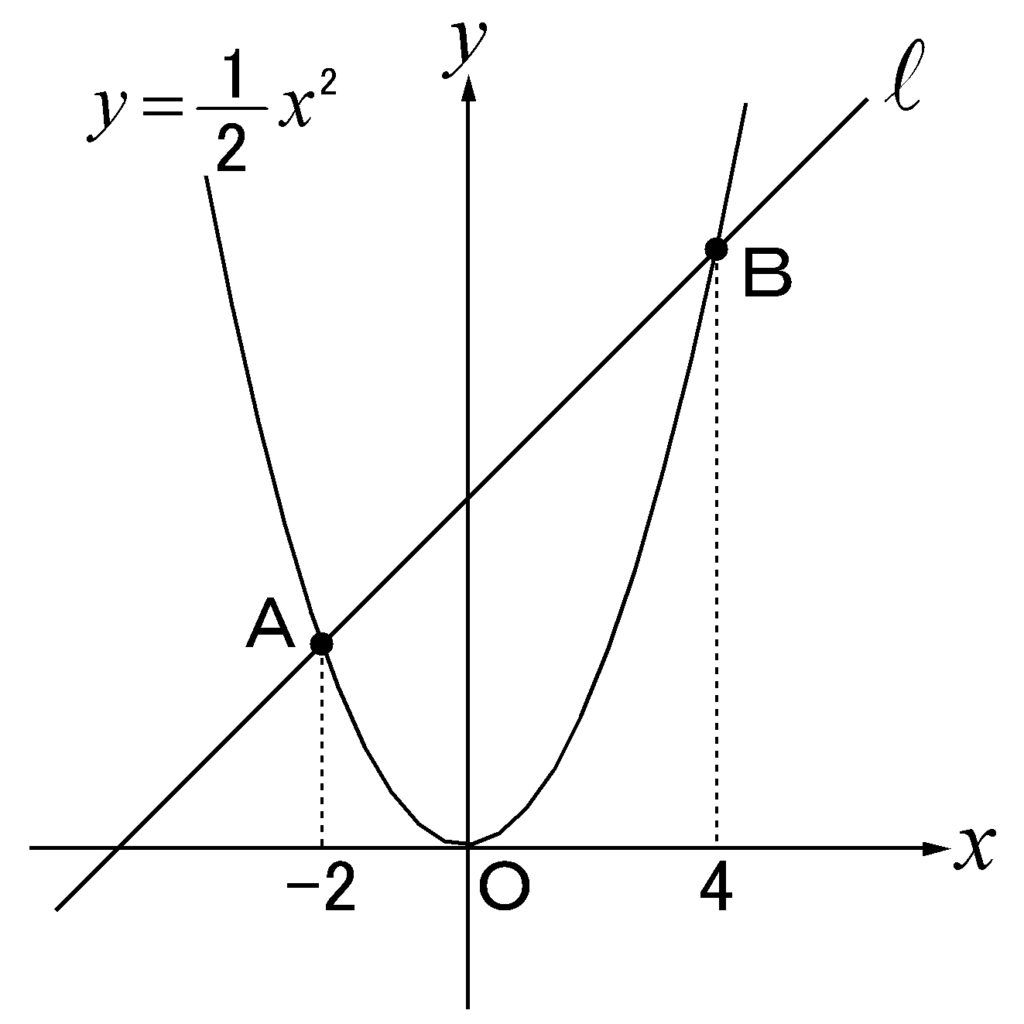
このとき、直線ABの式を求めるために皆さんでしたらどう求めますか?
おそらく多くの中学3年生がAとBのy座標を求めて連立方程式から傾きと切片を出すと思います。
※もしくは変化の割合から傾きを求めて切片を出すかと思います
ここで公式です!実はそれぞれのy座標を求めなくても、一瞬で直線ABの式を求めることができます!
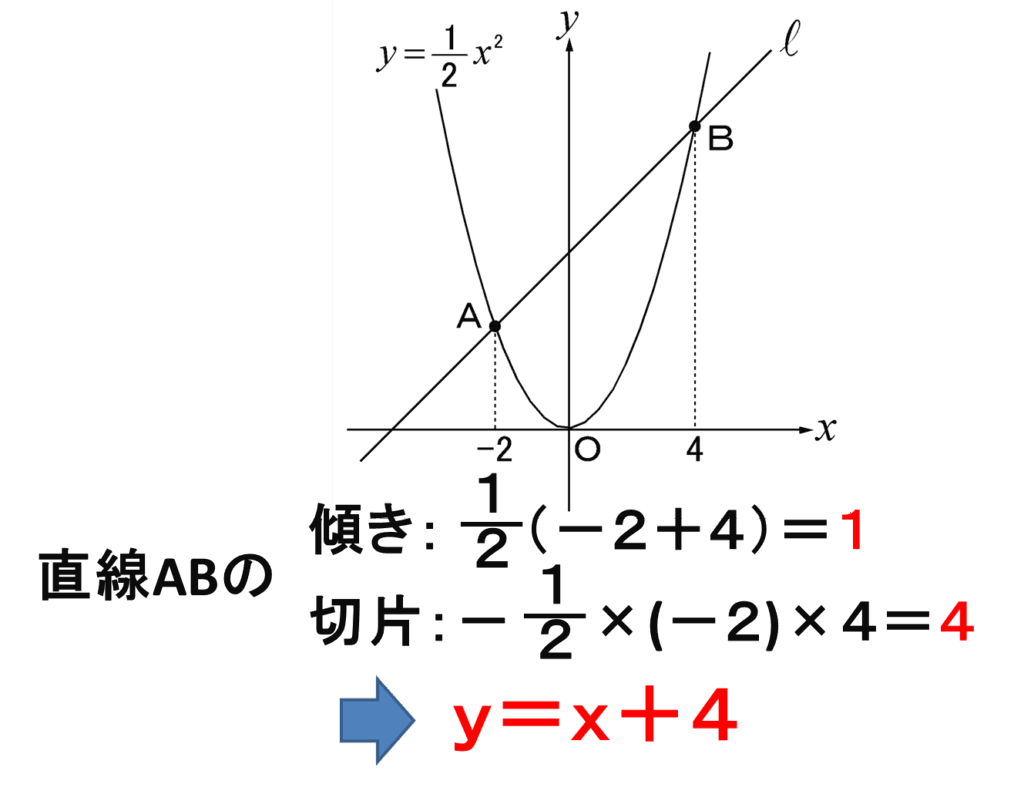
つまり二次関数をy=ax2、それぞれのx座標をpとqとしたとき、
傾きはa(p+q)、切片は-apqで求めることができます!
つまり、y=a(p+q)X-apqと公式化することが可能です!以下、軽く証明です。
1. 傾きがa(p+q)になる証明
一次関数では変化の割合は常に一定で、傾きと等しくなります。
つまり、この傾き(変化の割合)を二次関数の放物線で求めて、代用することが可能なのです!
今一度、二次関数の変化の割合の公式を復習しておきましょう。
【数学】二次関数の変化の割合!公式を利用して一瞬で求められるようにしよう!
これで直線ABの傾きは一瞬で求めることができました。
2. 切片が-apqになる証明
二次関数の式と2つの座標を文字で一般化しましょう。
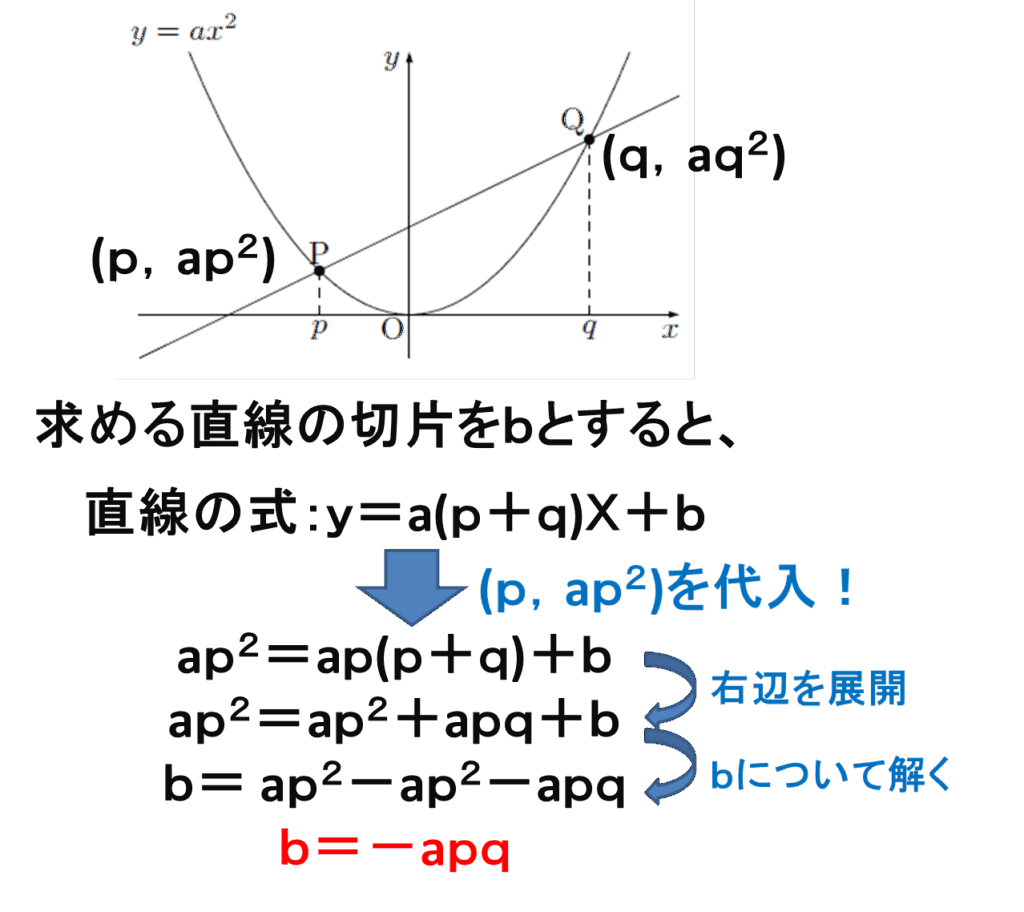
分配法則、等式の変形ができれば自力でここまで証明ができます!
※代入する座標はQ(q,aq2)でも同様な証明ができます
結果を使いこなすことも大事ですが、証明も同じくらい重要です!
きちんと理解することで応用力が身に付きますよ。
まとめ
以上、一次関数の直線の式を一瞬で求める裏技の紹介でした。
上記のような便利な公式は、100%静岡市の中学校では教わりません!
またWINGS以外の他塾でも教わることはほぼないかと思います。
知っておくととても便利な公式なので、
このブログを最後までご覧になった勉強意識の高いあなたは、是非使いこなしてみてください!
約1ヶ月後、後期中間テスト頑張ってくださいね。
今回のブログで少しでもご興味をお持ちいただけた方、是非WINGSの授業を体験してみてください!
学習相談・無料体験から受け付けておりますので、まずは気軽にホームページから資料請求をしてください。
お問い合わせはホームページの問い合わせフォーム、または054-330-9913までお願いします。
ブログを見ました・友達から聞きました・看板を見ました・チラシを見ました。とお伝えください。
【↓新年特別キャンペーン実施中↓】


