【高校数学Ⅰ】新高１へ！式の展開の序盤の壁！～置き換えと４つの式の展開～

静岡市葵区・駿河区で塾をお探しの皆さん。こんにちは！

思考力学習・ミス防止を徹底指導。集団指導の学習塾WINGSです。

葵小・横内小・竜南小・城北小・伝馬町小・安東小・静大附属小・服織小

城内中・東中・安東中・末広中

静岡東高校・静岡学園高校・静岡大成高校の方々にお世話になっております。

WINGSの新高１トリオが頑張っております！

中３の時から見てきましたが、少し風貌が変わってきましたね。

序盤の壁！高校数学の式の展開

高校での数学は、はじめは中学内容の復習⇒プラスアルファの応用といった感じで進んでいきます。

※上位校になればなるほどペースは速いです

その中で中３で習った簡単な式の展開から置き換え、その先の応用問題までを本日ブログで解説します！

【大前提】(x+y+3)(x+y+5)を展開しなさい。

上記の問題は解けますよね？共通部分の x+y をＭなどの文字で置き、

(M+3)(M+5)を展開し、最後にMを x+y に戻すだけです。

以下、そのやや応用版を解説していきます。

1. 置き換えの発展問題

少し考えてみてください。１つ前の問題と異なり、『…あれ？』と困るはずです。

それぞれの項はほとんど同じなのに符号が異なるため共通部分を文字で置けないのです！

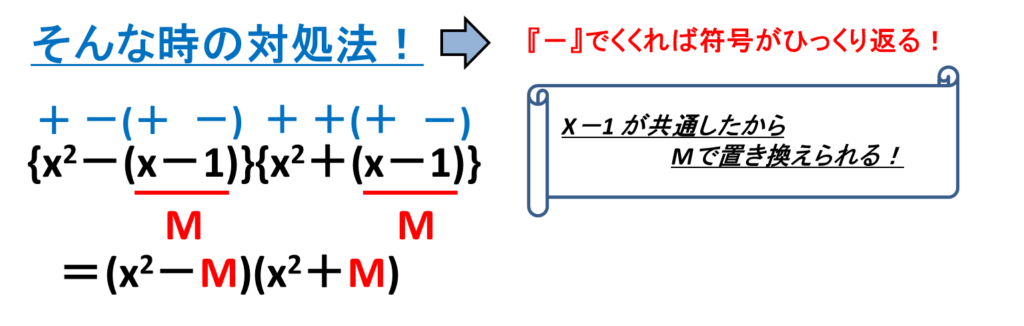
あとはいつもと同様に計算するだけです。

2. ４つの式の展開

地道に左から計算すれば何とかなりますが、それはスマートではありません…

しかし試しに少しだけ計算してどんな仕掛けがあるのかを確かめることは重要です！

実際に計算をして実験してみることでこういった法則的なことに気付けます。

次は組み合わせを変えてみましょう。

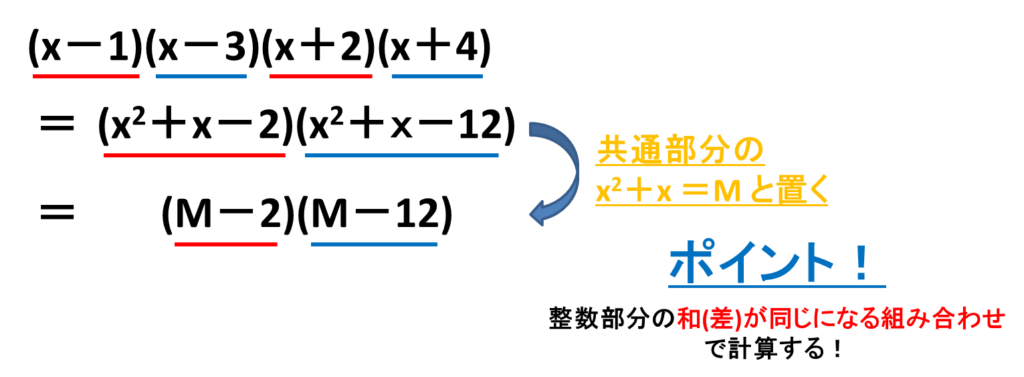
同様に計算を進めていき、最後にMを戻します。

まとめ

置き換えがしにくい計算問題においては、

カッコの中でも『－』でくくり符号を全て入れ替える。

また４つの式の展開に関しては、

和(差)が同じになる組み合わせで計算することで共通部分が出てきて文字置きが可能。

この先は因数分解の応用、３乗の展開公式ととにかく計算練習が必要になります。

ご自分の力だけでは心配な方、是非塾の力を借りて効率の良い勉強時間を確保しましょう！

今回のブログで少しでもご興味をお持ちいただけた方、是非WINGSの授業を体験してみてください！

学習相談・無料体験から受け付けておりますので、まずは気軽にホームページから資料請求をしてください。

お問い合わせはホームページの問い合わせフォーム、または054-330-9913までお願いします。

ブログを見ました・友達から聞きました・看板を見ました・チラシを見ました。とお伝えください。

【↓WINGSの詳細はコチラ↓】